
« La 8ème merveille du monde » aurait, un jour, énoncé le célèbre physicien, Albert Einstein. Cette mécanique et un formidable outil en phase de création de patrimoine. Nous allons voir dans cet article à quoi correspond la mécanique des intérêts composés et comment la mettre à profit dans le cadre d’une stratégie globale d’investissement.
Les intérêts simples
Avant d’entrer dans le détail, il me semble nécessaire d’introduire la notion d’intérêts simples. Prenons un exemple et imaginons un placement qui rapporte 2% par an. Si mon investisseur injecte 10 000 €, il récupère 200 € à la fin de l’année. L’année suivante, les 200 € ne capitalisent pas et rapporteront toujours le même intérêt.
Les intérêts composés
Comme son nom l’indique, les intérêts composés sont des intérêts capitalisés. Ils se cumulent au fil des années à partir d’un capital de départ. Prenons un exemple : vous investissez 100 € par mois à 10%. La première année vous gagnez 10€. L’année suivante, les 10% vont se calculer sur un capital plus important, à savoir 110 € et ainsi de suite jusqu’à créer un effet « boule de neige ».
Ainsi, vous comprenez que les intérêts se calculent sur un capital toujours plus important ce qui engendrera plus d’intérêts et donc plus de capital… et donc plus d’intérêts.
Pour utiliser ce mécanisme et le mettre à profit, il convient d’intégrer trois éléments :
- La durée d’investissement
- Le rendement de l’investissement
- Le capital investi
La durée et le rendement
Ces deux variables ont un impact exponentiel. Autrement dit, plus la durée d’investissement est longue, plus le rendement de l’investissement est important et plus le capital à terme sera considérable.
Le chiffre 72
Un moyen simple de connaître le temps nécessaire pour qu’un capital double et d’utiliser le chiffre 72. Prenez ce chiffre, et divisez-le par le rendement escompté d’un placement. Le livret A, qui rapporte 1%, vous obligera à attendre 72 ans de votre vie pour voir le capital doubler. Investissez en bourse, et votre capital doublera tous les 10 ans environ (7% par an étant la moyenne des marchés boursiers). Vous devez investir dans des placements financiers à forte valeur ajoutée pour vous permettre d’accroitre votre capital bien plus rapidement. Le livret A, pour ne citer que lui, doit être utilisé seulement pour faire face à des dépenses imprévues.
S’agissant de la durée d’investissement, investir le plus tôt possible, même de petites sommes, est primordial. Pour illustrer mes propos, je vais faire intervenir deux frères : Pierre et Paul. Le premier, souhaite se constituer un capital pour sa retraite et épargne 500 € par mois dès l’âge de 20 ans. Le second, plus préoccupé par les soirées étudiantes et sa volonté de se faire plaisir, n’épargne pas. À l’âge de 40 ans, Pierre dispose un capital de 120 000 € (sans prendre en compte les intérêts générés). Paul lui, n’a aucun capital. Ce dernier langui son frère et se met à épargner la même somme (500 €) jusqu’à sa retraite à 65 ans. Pierre, à 40 ans, pour diverses raisons, n’épargne plus. À l’âge de 65 ans, Pierre a alors un capital plus important que Paul, mais en prenant en compte les intérêts, la différence est incroyablement importante.
Tous les deux ont investi au sein d’un placement qui leur ont rapporté 7% annuel. Au terme, Paul se retrouve avec un capital de 1 380 000 € alors que Pierre n’a « que » 390 000 €. Soit un écart de presque 1 million entre les deux. Pierre a quasiment perdu 50 000 € pendant les 20 premières années de sa vie à ne pas épargner.
Une telle différence provient simplement du fait que Paul a su mettre de côté au début de sa vie active. À 40 ans, même s’il coupe ces versements, son capital travail pour lui et la mécanique des intérêts composés s’enclenche.
Conclusion : rattraper le temps perdu coûte très cher…

Le capital investi
Ce dernier paramètre à un impact linéaire. Investir la même somme chaque mois sans rendement n’aura pas de portée exponentielle sur le capital à terme.
Ainsi, un faible effort d’épargne mensuel vous offrira l’opportunité de vous constituer un capital conséquent.
Visualisons ensemble le capital à terme avec un montant de 100 € par mois :
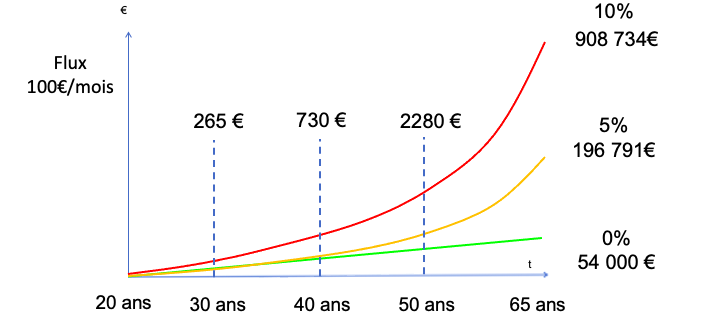
Que constate t’on ?
La courbe verte correspond à une épargne sur un compte courant. Celle-ci est linéaire, car il n’y a aucun rendement donc pas d’effet exponentiel. On pourrait aller plus loin en faisant apparaître l’inflation. En période de hausse des prix, il y a une perte de pouvoir d’achat et la courbe verte devient décroissante. La courbe jaune s’apparente davantage à un investissement au sein d’une assurance-vie avec un profil plutôt équilibré. La courbe devient exponentielle grâce au rendement procuré par l’investissement et au temps. En effet, il a fallu 45 ans à notre investisseur pour se constituer un patrimoine d’environ 196 000 € avec seulement un effort d’épargne de 100 € par mois.
Enfin, la courbe rouge nous montre une belle exponentielle grâce à la forte rentabilité de 10% et au temps. Le capital à terme est d’environ 908 000 € (54 000 € de capital et 854 000 € d’intérêts). Là aussi, le rendement est deux fois plus élevé que le placement à 5%, mais le capital final est plus que deux fois plus important : c’est l’impact exponentiel des intérêts composés.
Par ailleurs, et cela rejoint mon exemple de Pierre et Paul, plus vous commencez à investir tôt et plus l’effort d’épargne à réaliser est faible. En effet, pour obtenir les sommes finales, un investisseur qui entreprendrait d’investir à 40 ans devra épargner 730 € par mois et même 2280 € s’il démarre l’investissement à 50 ans !! Débutez le plus tôt possible, et les intérêts composés travailleront pour vous.
Que retenir de cette mécanique ?
Pour profiter de cette formidable mécanique, il convient de commencer à investir le plus tôt possible sur des solutions d’investissements. Ces dernières doivent vous offrir des rentabilités au moins supérieur à l’inflation pour vous protéger d’un risque de perte en capital. En effet, cela marche aussi dans les deux sens. Une inflation supérieure à votre taux de rendement aura un impact négatif !!
Régularité et patience sont les maîtres mots pour faire fonctionner les intérêts composés.
